科學是從信仰開始的，或者說是從幻想開始的。這在很大程度上使得我們堅信，能夠確定地描述這個世界，而絲毫不用牽涉到我們自己。——海森堡
波函數實際上是量子力學的一個基本假設，很多人誤以為它是數學推導的結果。
波函數假設是量子力學中最為基礎的概念，如光速不變原理作為狹義相對論的基礎公設一樣，貫穿於整個量子力學的始終。波函數最簡單的形式是：ψ(x)=Ae^i(p/)x，它是一種復指數函數，表示了粒子在某位置的概率幅，其絕對值的平方意味著某個時間點自由粒子在某個位置的可能性。
波函數的由來
波函數是描述微觀尺度範圍內物質行為的函數，來源於電子的雙縫幹涉實驗（上一篇內容），該實驗是量子力學最初的密碼，因為它揭示了電子的波動性，為了描述這種非粒子性行為，科學家引入了宏觀物理波（水波等機械波）的餘弦概念cos(x)，但是電子具有形體，不能在空間中若隱若現，也不應該偏好任何位置x，所以自由電子的運動不符合這種數學形式。於是，玻恩提出了概率波詮釋，認為波函數表徵了粒子位置的可能性，並不是描述粒子的軌跡，為了很好地符合概率這一理念，最終引入了波函數的復指數形式e^ix，故|e^ix|=|cosx+isinx|=1，意味著自由粒子在空間中運動時概率處處相等，不會出現起伏，遵循了物理的實在性原則。
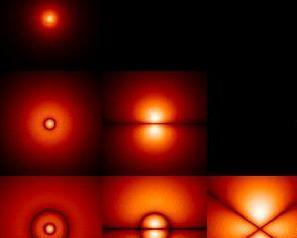氫原子電子云的概率密度波函數的含義
波函數的含義主要包括兩點：有限性和離散性。
波函數既然代表了不同位置的概率密度，那麼對其絕對值的平方進行全空間積分，結果一定是1，因為電子是真實存在於空間之中的。於是有：
∫|ψ(x)|dx=1
通過上式，可以確定ψ(x)中的係數A，就是我們熟知的波函數歸一化。這暗示了宇宙的有限性，因為無限的空間是無法計算歸一化的，所以只能假設宇宙大而有限，剛好符合了宇宙大爆炸模型。
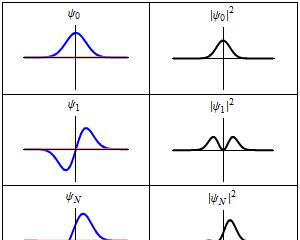描述諧振子的三個波函數宇宙是有限的，波函數ψ(x)也是有限無界的函數，那麼它一定是循環的，因此波函數必須符合周期條件：
ψ(x+L)=ψ(x)
千萬不要小看這個條件，因為把波函數ψ(x)=Ae^i(p/)x代入上式之後，直接可以導出動量p=2πm/L，這說明動量不是連續的，只能取整數倍的，意味著世界的離散性。
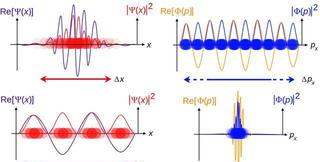一維自由粒子的波函數波函數終究是一種假設，其準確性及適用性只有通過實驗不斷地加強。這就好比，太陽從東方升起，在之前的99天確實如此，那麼我們就有理由相信明天依然成立的可能性≥99%。
日出東方隨著各種量子實驗的證實，量子糾纏、量子密鑰以及量子計算機的發展，科學家們對波函數的準確性深信不疑，同時也冒著巨大的風險，因為只要有一次實驗失敗，置信度就降為零。不過無論如何，波函數的理論已經成功，量子力學也已然輝煌。如同牛頓力學定律F=ma，即使被狹義相對論的新定律F=(dv/dt)*m/√(1-v/c)推翻，其地位也仍然是舉足輕重。
上一篇三分鐘讀懂量子力學：揭秘雙縫幹涉現象，下一篇三分鐘讀懂量子力學：什麼是不確定性原理。